【中学数学】三角形の合同証明を書くコツ
三角形の合同証明を書くコツ
中学2年生では、冬頃から図形の合同に関する学習が始ります。その中でも、合同の証明問題でつまずく生徒がいます。これまでの中学1年の数学では、図形問題であっても面積や体積求める問題だったので、小学校の延長線上のような学習でしたが、この証明問題は文章で説明するという、今までにやったことがない類の問題なので、戸惑ってしまうのかもしれません。しかし、解き方をしっかり理解すれば、誰でもできるようになるはずです。まずは基本となる、三角形の合同証明について、順番にポイントを説明していきます。
①仮定と結論を明確にする
【例題】
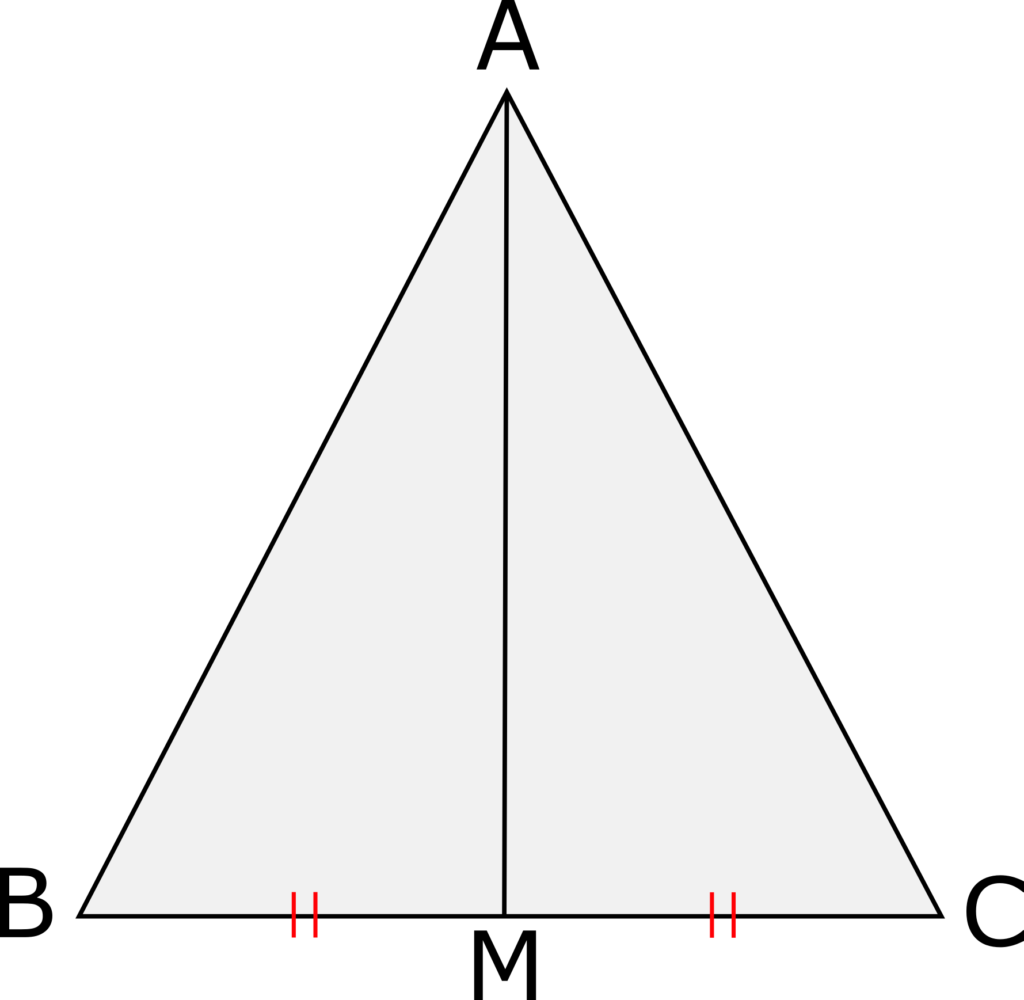
右の図においてBM=CM、∠AMO=∠AMCのとき、△ABM≡△ACMを証明しなさい。
仮定は「問題からわかっている事」で、結論は「証明したい事」です。まずはこの2つをはっきりさせておくことが大切です。この例題であれば、仮定と結論は以下のようになります。
仮定:BM=CM、∠AMO=∠AMC
結論:△ABM≡△ACM
「〇〇であれば」「○○のとき」「○○のように考える」というような内容が仮定です。結論は「□□を証明しなさい。」と、はっきり最後に書かれていることが多いので、見つけやすいはずです。ここで、結論を仮定に含めてしまわないように注意してください。これはできる人でも、ミスする可能性があるポイントです。仮定と結論を明確にすることが、1つ目のポイントです。
※仮定として判明している等しい辺や角は、図に印を付けておくと良い。結論の内容は図に書き込まないようにしよう。
②仮定以外の等しい辺や角を見つける
たいていの問題で、仮定で示された情報だけでは証明することができません。証明に必要な情報を、いくつかは自分で見つける必要があるのです。よく使われる等しい辺や角を、右のリストにまとめました。このリストは、気を付けて欲しい順に、上から並べています。なので、まずは共通の角や辺(重なっている角や辺)を探しましょう。先ほどの例題でも、AMは左右の三角形のどちらの辺でもあるので、AM=AMと書くことができます。共通の辺や角がなければ、対頂角や錯角を探しましょう。このように、仮定以外では、辺より角の方が等しい部分が多くあるのです。
等しい辺や角
- 共通の角、共通の辺は等しい
- 対頂角は等しい
- 平行線の錯角は等しい
- 平行線の同位角は等しい
- 二等辺三角形の2辺、底角は等しい
- 平行四辺形の対辺、対角は等しい
③書き始める前に合同条件を決める
三角形の合同条件は、すぐに出てくるように完璧に暗記しましょう。合同条件を書くのは、証明の最後の方になることが多いですが、合同条件は証明を書き始める前に決めておくようにしましょう。問題をしっかり読み、等しい辺や角の情報を出し、「この合同条件で証明できる。」という状態にしてから、証明を書き始めるのです。そうすると、結論までの道筋が大体見えているので、それを正確に言葉で表すだけになります。
三角形の合同条件
①3組の辺がそれぞれ等しい
②2組の辺とその間の角がそれぞれ等しい
③1組の辺とその両端の角がそれぞれ等しい
④証明の型をおぼえる
先ほどの例題の証明を実際に書いてみます。
△ABMと△ACMにおいて
仮定より
BM=CM・・・①
∠AMB=∠AMC・・・②
共通な辺なので AM=AM・・・③
①②③より2組の辺とその間の角がそれぞれ等しいので△ABM≡△ACM

2つの三角形が合同であることを証明するには、まず初めに「△ABMと△ACMにおいて」というように、2つの三角形のこととで説明することを明示します。あとは等しい辺や角を書き、合同条件により合同が成り立つことを書けば良いのです。ただし、等しい辺や角を示すときには、なぜ等しいかを書く必要があります。仮定であれば、「仮定より」という文言だけでいいのですが、そうでない場合は、丁寧に理由を書きましょう。
証明の書き方で注意するポイント
証明を書くときには、特に以下のことに注意してください。
錯角の書き方に注意
「錯角のため∠ABD=∠CDB」といった書き間違いをよく見かけます。正しくは「平行線の錯角のため∠ABD=∠CDB」もしくは「AB//CDで、錯角のため∠ABD=∠CDB」と書かなければなりません。平行線の錯角でなければ、等しいと言えないので、そこをきちんと明記する必要があるのです。
角は3点で表す
先ほどの例題では「∠A」という表記を使ってはいけません。なぜなら、∠Aには∠BAM、∠CAM、∠BACの3つが存在するため、どの角のことを指しているかわからないからです。角を記述するときは、基本的に3点を明記して表しましょう。
辺や角の書き順を合わせる
辺BMと辺MBは同じ辺を指していますが、合同を証明する場合、2つの図形の対応する順に書くようにしましょう。例えば、先ほどの例題で「BM=CM」と書きましたが、これは△ABMのBが、△ACMのCと対応する(重なる)頂点なので、同じ順番に書くということです。これを間違えて証明自体が不正解になるわけではありませんが、学校の先生によっては減点されることもあります。何より、普段から丁寧に証明を書き、合同な図形を意識することを徹底しておいて損はありません。